Lösungen:
4.1
-
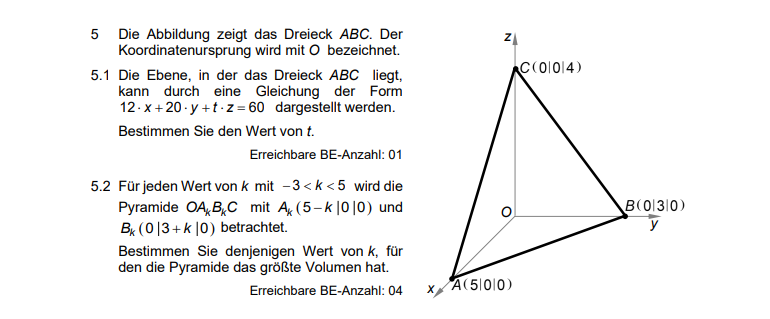
Die Gleichung der Ebene lautet:
-
12x + 20y + tz = 60
-
Wie setzen die Koordinaten der Punkte A (5 | 0 | 0), B (0 | 3 | 0) und C (0 | 0 |4) in die Gleichung ein:
-
Punkt A (5 | 0 | 0): 12(5) + 20(0) + t(0) = 60 => 60 = 60
-
Punkt B (0 | 3 | 0): 12(0) + 20(3) + t(0) = 60 => 60 = 60
-
Punkt C (0 | 0 | 4): 12(0) + 20(0) + t(4) = 60 => 4t = 60 |: 4 -> t = 15
-
t ist gleich 15.
-

-
Wir setzen die Koordinaten von A in den Verktorausdruck für g ein und prüfen, ob es einen Wer für den Parameter s gibt.
Die Gerade g ist gegeben durch:
-
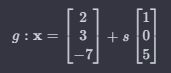
-
Setzen wir s = 0, um den Punkt auf der Geraden zu erhalten:
-
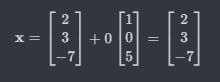
-
Die Koordinaten des Punkts A sind (4 | 0 | 0).
-
Da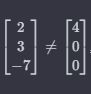 liegt
liegt
der nicht auf der Geraden g.
-
Die Koordinaten von A stimmen nicht mit den Koordinaten eines Punkts auf der Geraden g überein, daher liegt A nicht auf g.
-
4.2

-
Wir setzen die Koordinaten von A in den Verktorausdruck für g ein und prüfen, ob es einen Wer für den Parameter s gibt.
Die Gerade g ist gegeben durch:
-
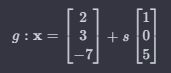
-
Setzen wir s = 0, um den Punkt auf der Geraden zu erhalten:
-
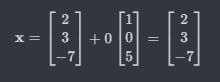
-
Die Koordinaten des Punkts A sind (4 | 0 | 0).
-
Da
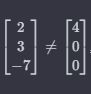 liegt
liegtder nicht auf der Geraden g.
-
Die Koordinaten von A stimmen nicht mit den Koordinaten eines Punkts auf der Geraden g überein, daher liegt A nicht auf g.
-
4.2
-
Um den Gemeinsamen Punkt der Geraden g und h zu finden, setzen wie die Gleichungen der beiden Geraden gleich und lösen nach s bzw. b auf.
-
Die Gerade g ist gegeben durch:
-
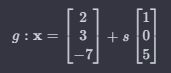
-
Die Gerade h geht durch die Punkte A (4 | 0 | 0) und B (5 | 1 | b) und kann in Parameternform geschreiben werden als:
-
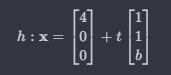
-
Jetzt setzen wir die Gleichungen der beiden Gerade gleich:
-
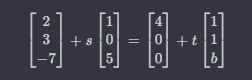
-
Vergleichen die entsprechenden Komponenten:
-
2 + s = 4 + t
3 = t
-7 + 5s = b
-
Da wir nun t kennen, setzen wir t = 3 in die erste Gleichung ein:
-
2 + s = 4 + 3 => Daraus ergibt sich s = 5.
-
Wir setzen s und t in die dritte Gleichung ein:
-
-7 + 5(5) = b
-
Wir lösen diese Gleichung:
-7 + 25 = b => b ist gliech 18.
Um den Gemeinsamen Punkt der Geraden g und h zu finden, setzen wie die Gleichungen der beiden Geraden gleich und lösen nach s bzw. b auf.
-
Die Gerade g ist gegeben durch:
-
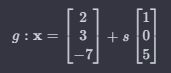
-
Die Gerade h geht durch die Punkte A (4 | 0 | 0) und B (5 | 1 | b) und kann in Parameternform geschreiben werden als:
-
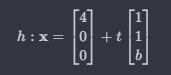
-
Jetzt setzen wir die Gleichungen der beiden Gerade gleich:
-
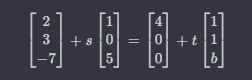
-
Vergleichen die entsprechenden Komponenten:
-
2 + s = 4 + t
3 = t
-7 + 5s = b
-
Da wir nun t kennen, setzen wir t = 3 in die erste Gleichung ein:
-
2 + s = 4 + 3 => Daraus ergibt sich s = 5.
-
Wir setzen s und t in die dritte Gleichung ein:
-
-7 + 5(5) = b
-
Wir lösen diese Gleichung:
-7 + 25 = b => b ist gliech 18.
-
5.1
5.1
-

-
Die Gleichung der Ebene lautet:
-
12x + 20y + tz = 60
-
Wie setzen die Koordinaten der Punkte A (5 | 0 | 0), B (0 | 3 | 0) und C (0 | 0 |4) in die Gleichung ein:
-
Punkt A (5 | 0 | 0): 12(5) + 20(0) + t(0) = 60 => 60 = 60
-
Punkt B (0 | 3 | 0): 12(0) + 20(3) + t(0) = 60 => 60 = 60
-
Punkt C (0 | 0 | 4): 12(0) + 20(0) + t(4) = 60 => 4t = 60 |: 4 -> t = 15
-
t ist gleich 15.
-
-
-