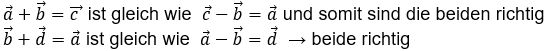Lösungen:
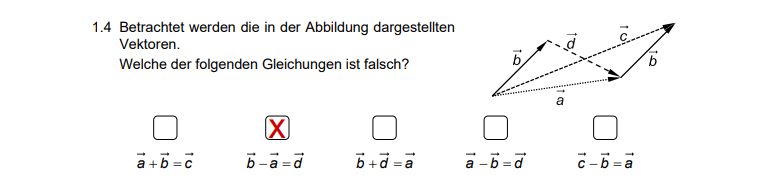
1.4
1.5

-
Die gegebene Ebene E: 3x + 4y = 7 hat die Form Ax + Bx + Cx = D, wobei A=3, B=4, C=0 (da kein z-Term vohanden ist), und D = 7.
Die Ebene verläuft durch den Koordinatenursprung.
-
Um zu überprüfen, ob die Ebene durch den Ursprung verläuft, setzen wir x = y = z = 0 in die Gleichung ein.
3(0) + 4(0) = 0 ist nicht gleich 7
Die Ebene verläuft nicht durch den Koordinatenursprung.
Die Ebene verläuft parallel zur z-Achse.
-
Da kein z-Term vorhanden ist (der Koeffizient C = 0), ist die Ebene parallel zur z-Achse.
Die Ebene schneidet alle drei Koordinatenachsen.
-
Um die Koordinatenachsen zu schneiden, muss die Ebene die Gleichungen x = 0, y = 0 und z = 0 erfüllen.
Wir setzen x = 0: 3(0) + 4y = 7. Es hat keine Lösung für y, daher schneidet die Ebene nicht die y-Achse.
Wir setzen y = 0: 3x + 4(0) = 7. Es hat keine Lösung für x, daher schneidet die Ebene nicht die x-Achse.
Wir setzen z = 0: Die Gleichung ex + 4y = 7 hat eine Lösung für x und y, daher schneidet die Ebene die z-Achse.
Die Ebene kann auch durch die Gleichung x + y = 1 beschrieben werden.
-
Wie setzen x + y = 1 in die Gleichung 3x + 4y = 7 ein:
3(1) + 4(0) = 3
Die Gleichung x + y = 1 beschreibt die Ebene nicht, da sie einen anderen Funktionsausdruck hat.
Die Ebene verläuft parallel zur x-y-Ebene.
-
Da kein z-Term vorhanden ist (der Koeffizient C = 0), ist die Ebene parallel zur x-y-Ebene.
-
1.5
-

-
Die gegebene Ebene E: 3x + 4y = 7 hat die Form Ax + Bx + Cx = D, wobei A=3, B=4, C=0 (da kein z-Term vohanden ist), und D = 7.
Die Ebene verläuft durch den Koordinatenursprung.
-
Um zu überprüfen, ob die Ebene durch den Ursprung verläuft, setzen wir x = y = z = 0 in die Gleichung ein.
3(0) + 4(0) = 0 ist nicht gleich 7
Die Ebene verläuft nicht durch den Koordinatenursprung.
Die Ebene verläuft parallel zur z-Achse.
-
Da kein z-Term vorhanden ist (der Koeffizient C = 0), ist die Ebene parallel zur z-Achse.
Die Ebene schneidet alle drei Koordinatenachsen.
-
Um die Koordinatenachsen zu schneiden, muss die Ebene die Gleichungen x = 0, y = 0 und z = 0 erfüllen.
Wir setzen x = 0: 3(0) + 4y = 7. Es hat keine Lösung für y, daher schneidet die Ebene nicht die y-Achse.
Wir setzen y = 0: 3x + 4(0) = 7. Es hat keine Lösung für x, daher schneidet die Ebene nicht die x-Achse.
Wir setzen z = 0: Die Gleichung ex + 4y = 7 hat eine Lösung für x und y, daher schneidet die Ebene die z-Achse.
Die Ebene kann auch durch die Gleichung x + y = 1 beschrieben werden.
-
Wie setzen x + y = 1 in die Gleichung 3x + 4y = 7 ein:
3(1) + 4(0) = 3
Die Gleichung x + y = 1 beschreibt die Ebene nicht, da sie einen anderen Funktionsausdruck hat.
Die Ebene verläuft parallel zur x-y-Ebene.
-
Da kein z-Term vorhanden ist (der Koeffizient C = 0), ist die Ebene parallel zur x-y-Ebene.