Lösungen:
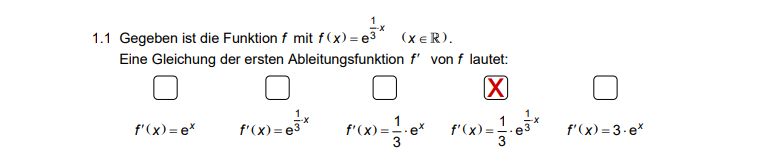
1.1
-

-
-Um die Ableitung der Funktion e^1/3*x zu finden, verwenden wir die Kettenregel. Die Kettenregel besagt, dass die Ableitung einer Verkettung
von Funktionen das Produkt der Ableitung der äußeren Funktion und der Ableitung der inneren Funktion ist.
1. Ableitung der äußeren Funktion:
Die äußere Funktion ist e^u, wobei u = 1/3*x. Die Ableitung davon ist e^u.
2. Ableitung der inneren Funktion:
Die innere Funktion ist u = 1/3*x. Die Ableitung davon ist 1/3.
-
Daher ist die erste Ableitung von e^1/3x gleich 1/3*e^1/3*x.
-
1.2

-Um die Ableitung der Funktion e^1/3*x zu finden, verwenden wir die Kettenregel. Die Kettenregel besagt, dass die Ableitung einer Verkettung
von Funktionen das Produkt der Ableitung der äußeren Funktion und der Ableitung der inneren Funktion ist.
1. Ableitung der äußeren Funktion:
Die äußere Funktion ist e^u, wobei u = 1/3*x. Die Ableitung davon ist e^u.
2. Ableitung der inneren Funktion:
Die innere Funktion ist u = 1/3*x. Die Ableitung davon ist 1/3.
-
Daher ist die erste Ableitung von e^1/3x gleich 1/3*e^1/3*x.
-
1.2
-

-
Ansatz: f (x) = f (x-a)^2 + b
a => Versschiebung des Graphen um n nach rechts/links
b => Verschiebung des Graphen um n nach oben/unten
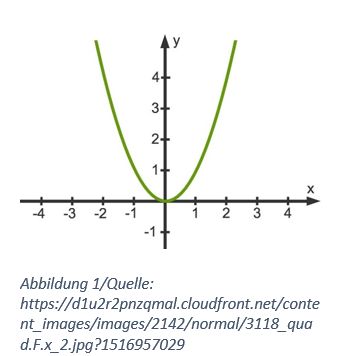
Allerdings wissen wir den Graph der Funktion f (x) = x^2 aussieht. Nähmlich
-
-
a = 2
b = -1
-
Werte einsetzen:
-
f (x) = (x-2)^2 - 1 => f (x) = x^2 - 4x + 4 -1 => f (x) = x^2 - 4x + 3
-
f' (x) = 2x - 4
-
-
Ansatz: f (x) = f (x-a)^2 + b
a => Versschiebung des Graphen um n nach rechts/links
b => Verschiebung des Graphen um n nach oben/unten
Allerdings wissen wir den Graph der Funktion f (x) = x^2 aussieht. Nähmlich
-

-
a = 2
b = -1
-
Werte einsetzen:
-
f (x) = (x-2)^2 - 1 => f (x) = x^2 - 4x + 4 -1 => f (x) = x^2 - 4x + 3
-
f' (x) = 2x - 4
-
-